Image d'un point lumineux dans un dioptre
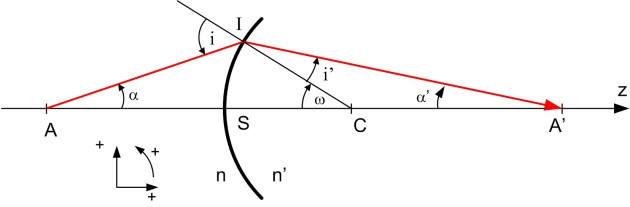
Considérons un dioptre sphérique séparant deux milieux d'indices \(n\) et \(n'\), défini par son centre de courbure \(C\), son sommet \(S\), son rayon de courbure \(R = \overline{SC}\).
Toutes les longueurs et les angles sont orientés en utilisant la convention de la trigonométrie.
Un point \(A\) est situé dans l'espace objet sur la droite \(SC\). Le rayon issu de \(A\) passant par \(S\) est perpendiculaire au dioptre, il n'est pas dévié. Un autre rayon issu de \(A\) passant par un point quelconque \(I\) du dioptre subit une réfraction le rayon émergent coupe \(SC\) en un point \(A'\).
Cherchons la position de \(A'\). Suivant la figure 12 :
\(i\) est l'angle d'incidence du rayon sur le dioptre
\(i'\) est l'angle de réfraction, et, d'après (5), \(n \cdot \sin(i) = n' \cdot \sin(i')\)
Une formule classique dans le triangle \(CAI\) donne :
\(\frac{ \overline{CA} }{ \sin ( \pi -i)} = \frac{ \overline{CA} }{ \sin (i)} = - \frac{ \overline{IA} }{ \sin ( \omega ) }\)
\(( \overline{CA}<0,\; \overline{IA}<0 ,\; \omega <0 ,\; i >0 )\)
On peut écrire aussi :
\(\frac{\overline{CA'}}{\sin (i')} = - \frac{\overline{IA'}}{\sin (\omega )}\)
et donc :
\(\frac{\overline{CA}}{\overline{CA'}} = \frac{\overline{IA} \cdot \sin (i)}{\overline{IA'} \cdot \sin (i')} = \frac{n \cdot \overline{IA}}{n' \cdot \overline{IA'}} \mbox{ (7)}\)
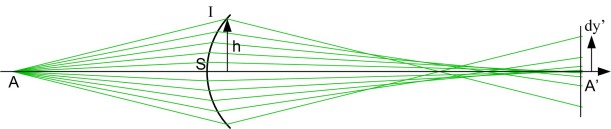
Le stigmatisme de la conjugaison voudrait que \(A'\) ne dépende pas de la position de \(I\). Il faut alors que \(CA'\) reste fixe de même que le rapport \(IA/IA'\). Ceci n'est obtenu que dans une position particulière de \(A\) et n'est pas réalisé dans le cas général.
La figure 13 montre concrètement un exemple de tracé de rayon dans un dioptre, l'aberration y est importante. Ce tracé est obtenu avec le logiciel gratuit Oslo-Edu téléchargeable à l'adresse : http://www.lambdares.com/downloads/index.phtml#osloedu
