Dimension des images, grandissement transversal, grandissement angulaire
Considérons un objet \(AB\) situé à une distance \(z\) du dioptre de rayon \(R\) dans un plan perpendiculaire à l'axe. Son image est \(A'B'\) à la distance \(z'\). Soient \(y = \overline{AB} \mbox{ et } y' = \overline{A'B'}\)
Dans l'approximation paraxiale suivant la figure 17 :
\(A'B'\) est perpendiculaire à l'axe
\(\theta\) est l'angle de champ objet, \(\theta\) étant petit, \(\tan (\theta) = \theta = y/z\)
De même, \(\theta '\) est l'angle de champ image et \(\theta ' = y'/z'\)
La réfraction en \(S\) du rayon partant de \(B\) est telle que : \(n \theta= n' \theta '\)
On en déduit la dimension \(y'\) de l'image :
\(y' = y \cdot \frac{nz'}{n'z}\)
et le grandissement transversal \(g_{y}\) :
\(g_{y} = \frac{\overline{A'B'}}{\overline{AB}} = \frac{y'}{y} = \frac{nz'}{n'z} \mbox{ (11)}\)
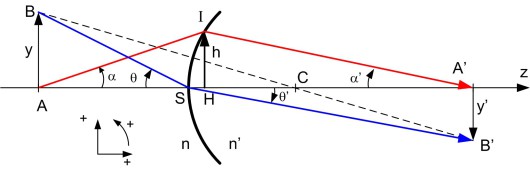
On définit, pour une conjugaison \((AA')\) donnée, un grandissement angulaire \(g_{\alpha} = \frac{\alpha '}{\alpha}\) entre les angles par rapport à l'axe de deux rayons conjugués passant par \(A\) et \(A'\).
Suivant la figure 17, I est l'intersection des rayons avec le dioptre et \(h= \overline{HI}\) la distance de \(I\) à l'axe. Dans l'approximation paraxiale, \(h\) est petit, la courbure du dioptre est négligée et \(H\) est supposé confondu avec \(S\). Nous avons :
\(\alpha = - \frac{h}{z} \mbox{ et } \alpha ' = - \frac{h}{z'}\)
On en déduit :
\(g_{\alpha} = \frac{\alpha '}{\alpha} = \frac{z}{z'} \mbox{ (12)}\)
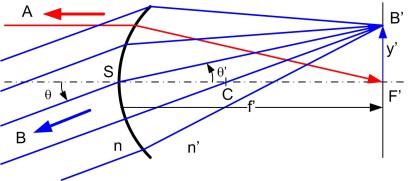
Dans le cas où l'objet \(AB\) est à l'infini, sa dimension transversale est donné par son angle de champ \(\theta\). Suivant la figure 18, \(A\) est sur l'axe, son image est \(F'\), \(B'\), image de \(B\) est dans le plan focal image à une distance\( y'\) de l'axe telle que :
\(y' = f' \cdot \theta ' = \frac{n}{n'} f' \cdot \theta = - f \cdot \theta\)