Système basé sur deux caméras
Principe
Dans la première partie la caméra était seule et la matrice P de la caméra, permet de passer des coordonnées de l'objet aux coordonnées de la caméra, repère dont l'origine est le centre optique de la caméra, le plan xy le plan image et l'axe z l'axe optique.
Nous avons maintenant deux caméras le repère globale sera centré sur la caméra 1 (caméra à gauche). Nous avons un second repère pour la caméra 2 (caméra droite). Il faut localiser la seconde caméra par rapport à ce repère et connaître son orientation. Cette localisation est complètement définie par la connaissance de la matrice homogène de passage de du repère caméra 1 au repère caméra 2.
Fondamental : Cas idéal : caméras identiques plans images confondus et axe optique parallèles séparées d'une distance b selon x
Les deux caméras sont caractérisées par leurs matrices intrinsèques ( caractéristiques physiques de la caméra) et leurs matrices extrinsèques, positionnement relatif des caméras.
Nous allons nous placer dans le cas le plus simple possible : les caméras sont identiques, même matrice intrinsèque, et les plans images sont confondus et les axes optiques sont parallèles et les caméras sont séparées d'une distance b selon l'axe x. Un objet de coordonnées [X Y Z 1]T est vu dans l'image 1 en [u1 v1 1]P et sur la caméra 2 en [u2 v2 1]T. La matrice de calibrage de la caméra 1 est donc :
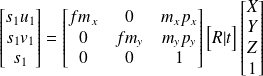
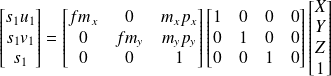
En calculant l'expression matricielle précédente on obtient deux équations :
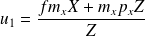 et
et
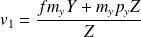
Pour la matrice de calibrage de la caméra 2 la seule différence est le vecteur translation :
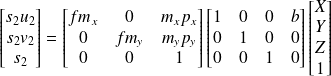
qui donne :
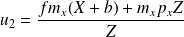 et
et
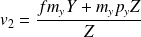
Dans ces équations [u1 v1 1]P et [u2 v2 1]T sont connus et on recherche [X Y Z 1]T. le système se résout simplement :
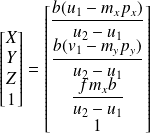
Dans les équations précédentes on remarque que v1=v2 . Cette propriété signifie que un point de l'espace est à la même hauteur sur les deux images. La recherche de correspondance entre les deux images est ainsi facilitée.
Ces équations permettent aussi de localiser un point dans l'espace connaissant leurs positions respectives dans l'image gauche et droite.
Remarque : Pourquoi ce cas est -il idéal ?
Dans le cas précédent les caméras sont identiques et séparées d'une distance b selon x. Les plans images sont confondus et les axes optiques sont parallèles. Ces conditions sont très difficiles à réaliser mécaniquement. La dimension du capteur est de l'ordre du centimètre. L centre du capteur doit passer par l'axe optique et la perpendiculaire à cette surface en ce point doit être l'axe optique. De plus en prolongeant le plan du capteur selon x on doit retrouver l'autre capteur vérifiant les mêmes conditions. Mécaniquement ces éléments sont impossibles à réaliser. De plus on peut en calibrant le système se ramener au cas idéal en utilisant une méthode de rectification.






