Contrainte épipolaire
Rappel : La matrice de calibrage d'une caméra
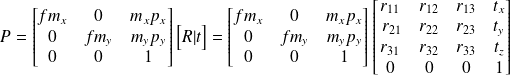
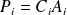avec Pi la matrice transformation perspectives Ci la matrice des paramètres intrinsèques et Ai la matrice des paramètres extrinsèques. En utilisant la matrice P, on trouve les coordonnées sur l'image d'un point de coordonnées X Y Z 1 de la scène :
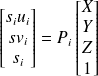
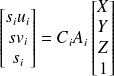
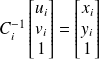
Relation entre l'image droite et gauche
Soit M=[X1 Y1 Z1 ] un point de l'espace dans le repère gauche et [X2 Y2 Z2] ses coordonnées dans le repère droit.
La relation liant les deux systèmes de coordonnées est la suivante :
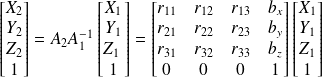
A1-1 nous permet de passer du repère de la caméra gauche au repère scène et A2 de la scène au repère de la caméra droite. On a
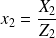et
et 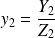de même pour
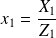et
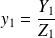
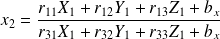
et
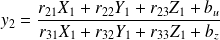
En posant m =[x y 1]T et r1=[ri1 ri2 ri3]les formules précédentes deviennent :
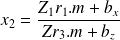et
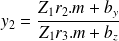
En utilisant cette dernière équation on trouve
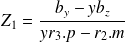et en substituant dans x2 on obtient la relation suivante :
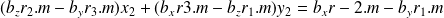Cette équation peut s'écrire plus simplement Ax2+By2=C où A, B et C sont des constantes dépendant de la géométrie.
Cela signifie qu'un point (x1,y1) de l'image gauche est sur une droite dans l'image droite.
