Projection perspective
Fondamental : Projection perspective : modèle de sténopé
Soit une image formée sur un plan et un point P du plan image appelé point principal. Soit une droite perpendiculaire à ce plan passant par F appelée axe optique.
Soit un point C de l'axe optique tel que
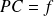où
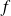est la distance focale et C est le centre de projection.
La projection par rapport C sur plan d'un point M de coordonnées
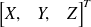est un point de coordonnées
.
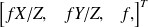En coordonnées homogènes cela se traduit par la formule matricielle suivante :
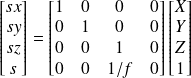
On peut multiplier la matrice par f sans changer le sens de la relation car nous travaillons en coordonnées homogènes :
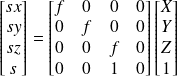
Les coordonnées cartésiennes de la projection de M sont (sx/s,sy/s,sz/s).
Rappel : Repère image-capteur Numérique
Une image numérique est un tableau de pixels comportant N lignes et M colonnes. L'origine est située en haut à gauche et l'axe des y est dirigé vers le bas (repère indirect). Le pixel, un élément photo sensible a une dimension physique qui est généralement de l'ordre du
.
 | D'après http://www.andor.com/scientific-cameras/neo-and-zyla-scmos-cameras/neo-55-scmos |
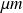Remarque : Transformation caméra image
Les coordonnées (u,v) dans le repère image sont mesurées en pixels. Le nombre de pixels par mm est ku selon u et kv selon v
Le point principal, intersection de l'axe optique avec le plan image, n'est pas en coïncidence avec l'origine des coordonnées de l'image. Il faut déplacer ce point d'une quantité (px,py,pz) :
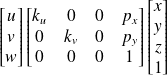
Définition : Matrice de calibrage de la caméra
On peut écrire globalement les expressions précédentes :
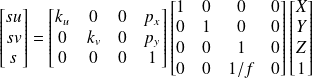
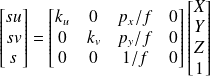
On peut multiplier tous les éléments par f (les coordonnées homogénes nous laisse cette possibilté)
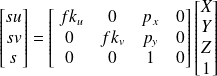
La matrice
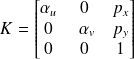est la matrice de calibrage de la caméra ou matrice intrinsèque avec
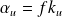et
.
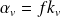Remarque : Origine du repère
L'origine du repère est le centre optique de la caméra et l'axe z est l'axe optique de la caméra.
Complément : Repère monde
En général la caméra n'est pas toujours l'origine du repère. Les coordonnées dans le repère caméra Xc et le repère monde Xw sont reliées par une rotation et une translation :
Xc = R(Xw-C) où C sont les coordonnées de la caméra dans le repère monde t et R une matrice de rotation représentant l'orientation de la caméra. Xw-C signifie que le centre de la rotation est le centre optique.
En coordonnées homogènes l'équation précédente s'écrit :
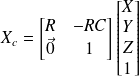
Définition : Coordonnées de la projection d'un point sur le plan image.
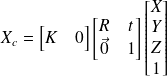avec t=-RC
Définition : Coordonnées de la projection d'un point sur le plan image. en pixel pour une caméra orientée
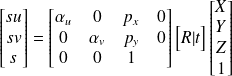
Fondamental : Matrice de projection perspective d'une caméra
En développant l'expression précédente on obtient une matrice P de 3 lignes et 4 colonnes :
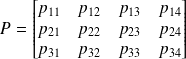
p34 est généralement fixé à 1 (contrainte due à la projection centrale)
Cette matrice permet de passer du repère de l'objet au repère image.
