

Next: LDA adiabatique
Up: Fonctionnelle de la densité
Previous: Fonctionnelle de la densité
Table des matières
Nous nous intéressons donc à la densité
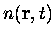 d'un système
d'électrons évoluant à partir d'un état initial fixé mais quelconque
d'un système
d'électrons évoluant à partir d'un état initial fixé mais quelconque
![[*]](foot_motif.gif)
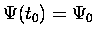 |
(33) |
sous l'influence d'un potentiel extérieur
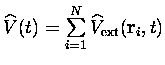 .
.
Les seules hypothèses consistent à demander que le temps 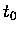 soit fini
et que le potentiel soit développable en série de Taylor autour de
soit fini
et que le potentiel soit développable en série de Taylor autour de
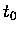 , sans contraintes sur le rayon de convergence.
On peut alors prouver des théorèmes de la forme de ceux de Hohenberg-Kohn
, sans contraintes sur le rayon de convergence.
On peut alors prouver des théorèmes de la forme de ceux de Hohenberg-Kohn
![[*]](foot_motif.gif) :
:
- 1.
- les densités
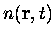 et
et
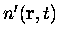 évoluant à partir
du même état initial
évoluant à partir
du même état initial 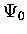 sous l'influence de deux potentiels
sous l'influence de deux potentiels
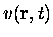 et
et
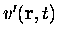 sont toujours différentes pourvu que
les potentiels diffèrent de plus qu'une fonction dépendant uniquement du
temps :
ainsi, il existe une correspondance biunivoque entre densité dépendant
du temps et potentiel dépendant du temps, à
sont toujours différentes pourvu que
les potentiels diffèrent de plus qu'une fonction dépendant uniquement du
temps :
ainsi, il existe une correspondance biunivoque entre densité dépendant
du temps et potentiel dépendant du temps, à 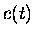 près. La fonction
d'onde dépendant du temps du système peut donc être considérée comme une
fonctionnelle de la densité dépendant du temps, à un facteur de phase
près :
près. La fonction
d'onde dépendant du temps du système peut donc être considérée comme une
fonctionnelle de la densité dépendant du temps, à un facteur de phase
près :
$](img388.gif) |
(34) |
par conséquent, la valeur moyenne de tout opérateur quantique
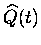 est une fonctionnelle unique de la densité :
est une fonctionnelle unique de la densité :
=\left\langle \widetilde{\Psi}[n](t)\Big\vert\widehat{Q}(t)\Big\vert\widetilde{\Psi}[n](t) \right\rangle$](img390.gif) |
(35) |
il est clair en effet que l'ambiguïté de phase disparaît.
- 2.
- Comme la solution de l'équation de Schrödinger dépendant du
temps :
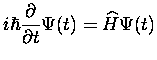 |
(36) |
avec le Hamiltonien de I.1 et la condition initiale de B.1
correspond à un extremum de l'action quantique, cette dernière devient
alors elle aussi une fonctionnelle de la densité et s'écrit
![$\displaystyle \mathcal{A}=\int_{t_0}^{t_1}\,dt \left\langle \widetilde{\Psi}[n]...
...tial}{\partial t}- \widehat{H}(t)\Bigg\vert\widetilde{\Psi}[n](t) \right\rangle$](img392.gif) |
(37) |
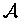 présente donc un extremum pour la densité dépendant du temps solution
de B.4.
présente donc un extremum pour la densité dépendant du temps solution
de B.4.
La densité s'obtient alors en résolvant l'équation d'Euler
![$\displaystyle \frac{\delta\mathcal{A}[n]}{\delta n({\bf r},t)}=0$](img394.gif) |
(38) |
avec les conditions aux limites appropriées.
En séparant la contribution du potentiel extérieur, on peut définir
une fonctionnelle universelle de la même façon que dans le cas statique.
De même, on peut établir des équations à un corps similaires au cas
statique. Le problème de la 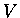 -représentabilité se pose alors : si nous
considérons le cas sans interaction mutuelle des électrons, le potentiel
extérieur
-représentabilité se pose alors : si nous
considérons le cas sans interaction mutuelle des électrons, le potentiel
extérieur
$](img63.gif) correspondant à une densité donnée
correspondant à une densité donnée
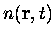 est unique. Rien n'assure cependant son existence pour une
densité arbitraire ; il faut donc supposer l'existence de
est unique. Rien n'assure cependant son existence pour une
densité arbitraire ; il faut donc supposer l'existence de
$](img63.gif) pour le système avec interaction. Alors, par un raisonnement
similaire au cas statique la densité du système peut être obtenue par
pour le système avec interaction. Alors, par un raisonnement
similaire au cas statique la densité du système peut être obtenue par
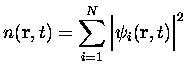 |
(39) |
avec les 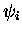 qui satisfont à l'ensemble d'équations
de Kohn-Sham dépendant du temps (TDKS) :
qui satisfont à l'ensemble d'équations
de Kohn-Sham dépendant du temps (TDKS) :
 \right] \psi_i({\bf r},t)$](img62.gif) |
(40) |
et on peut faire la même séparation de
$](img63.gif) que dans le
cas statique, c'est à dire définir
que dans le
cas statique, c'est à dire définir
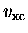 par
par
 = v_{\mbox{\scriptsize ext}}({\bf r},t) + \Phi({\bf r},t) +v_{\mbox{\scriptsize xc}}[n]({\bf r},t)$](img65.gif) |
(41) |
avec
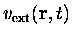 le potentiel extérieur et
le potentiel extérieur et
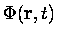 le potentiel coulombien classique.
Cependant, comme dans le cas statique, le problème de
départ B.4 n'a été en quelque sorte que reformulé : il faut
trouver une approximation de
le potentiel coulombien classique.
Cependant, comme dans le cas statique, le problème de
départ B.4 n'a été en quelque sorte que reformulé : il faut
trouver une approximation de
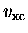 .
.



Next: LDA adiabatique
Up: Fonctionnelle de la densité
Previous: Fonctionnelle de la densité
Table des matières
Florent Calvayrac
1999-05-05
![[*]](foot_motif.gif)
![]() d'un système
d'électrons évoluant à partir d'un état initial fixé mais quelconque
d'un système
d'électrons évoluant à partir d'un état initial fixé mais quelconque
![[*]](foot_motif.gif)
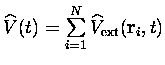 .
.
![]() soit fini
et que le potentiel soit développable en série de Taylor autour de
soit fini
et que le potentiel soit développable en série de Taylor autour de
![]() , sans contraintes sur le rayon de convergence.
On peut alors prouver des théorèmes de la forme de ceux de Hohenberg-Kohn
, sans contraintes sur le rayon de convergence.
On peut alors prouver des théorèmes de la forme de ceux de Hohenberg-Kohn
![[*]](foot_motif.gif) :
:
![]() est une fonctionnelle unique de la densité :
est une fonctionnelle unique de la densité :
=\left\langle \widetilde{\Psi}[n](t)\Big\vert\widehat{Q}(t)\Big\vert\widetilde{\Psi}[n](t) \right\rangle$](img390.gif)
![$\displaystyle \mathcal{A}=\int_{t_0}^{t_1}\,dt \left\langle \widetilde{\Psi}[n]...
...tial}{\partial t}- \widehat{H}(t)\Bigg\vert\widetilde{\Psi}[n](t) \right\rangle$](img392.gif)
![$\displaystyle \frac{\delta\mathcal{A}[n]}{\delta n({\bf r},t)}=0$](img394.gif)