Modèle du << jellium >>

En effet, la simplification la plus radicale que l'on puisse faire de la structure ionique de l'agrégat consiste à négliger complètement le détail de cette structure et à simplement considérer celle-ci comme un fond uniforme de charge positive. C'est le modèle du << jellium >>, qui trouve son origine en physique du solide. Dans un premier temps, on peut considérer ce jellium comme une sphère uniformément chargée ; c'est ce qu'a fait Eckardt dans le papier séminal [32] où il prédisait les nombres magiques des agrégats de sodium. Le seul paramètre est alors le rayon de l'agrégat, qui est déduit du rayon de Wigner-Seitz du métal.

Cette approximation brutale donne une mauvaise valeur pour la position de la résonance plasmon du nuage électronique, car elle simplifie trop les effets de surface ; le fond de charge positive passe ainsi discontinûment d'une valeur constante à zéro à la surface (<< jellium >> abrupt). Par conséquent, le nuage des électrons de valence qui s'étend un peu au delà de cette barrière (effet de << spillout >> ) à cause d'effets quantiques subit une force de rappel erronée, et la position du pic plasmon est trop élevée en énergie (on trouve par exemple 3.3 eV pour le cas typique de l'agrégat Na$_9^+$).

Il faut donc modifier cette surface ; la justification formelle consiste à considérer que les électrons de valence ressentent une forme moyenne du pseudopotentiel des ions. On obtient alors un << jellium >> adouci qui donne une position de la résonance plasmon conforme aux résultats expérimentaux. Cette modification a été inspirée par un modèle effectif d'oscillateur déformé avec potentiel de Woods-Saxon pour les agrégats dû à Clemenger et Nilsson : ce modèle ne tient pas compte des interactions électroniques.

Figure: Partie imaginaire de la transformée de Fourier du moment dipolaire d'un agrégat Na$_9^+$ obtenue avec un fond de << jellium >> adouci, d'épaisseur de surface 1 a$_0$, excitation dans le régime linéaire, calcul dans le domaine temporel de 10000 itérations de 0.1 unités Hartree (48 fs), filtrage de la transformée

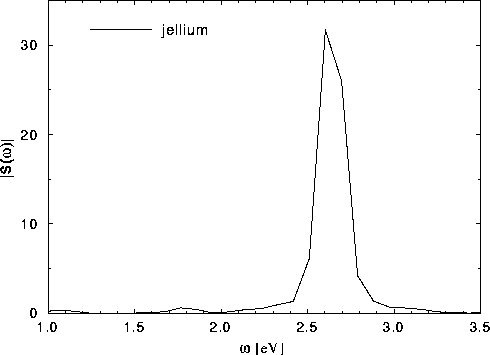
Nous donnons sur la figure I.1 le résultat obtenu par notre méthode pour la section efficace de photoabsorption pour Na$_9^+$ avec un tel fond ionique, que l'on peut comparer aux mesures expérimentales à très basse température de [33] présentées sur la figure III.3. page . On peut voir que la résonance plasmon est à la bonne énergie, mais il n'y a qu'un seul pic principal par rapport aux deux expérimentalement visibles. Nous reviendrons plus loin sur cette déficience. Le modèle du << jellium >> demeure néanmoins très intéressant pour le sodium, car lorsque l'agrégat est dans une phase liquide où les ions n'occupent pas des positions figées (à 300 K par exemple), seules les caractéristiques d'ensemble comptent, et un agrégat magique tel que Na$_9^+$ présente alors une forme d'ensemble sphérique qui se manifeste par un seul pic d'origine géométrique dans le spectre de photoabsorption. Il n'y a pas de pic secondaire d'origine quantique, car dans le modèle du << jellium >> pour cet agrégat, il n'y a pas de monoexcitation électronique d'énergie proche de celle du plasmon, donc pas d'interférence du point de vue de la RPA (cette question importante est discutée dans [19]), et le pic plasmon n'est pas fragmenté.

Les agrégats de sodium non-magiques donnent, eux, plusieurs pics dans les spectres de photoabsorption, y compris à des températures où l'agrégat est sans doute liquide (voir par exemple le cas de Na$_{11}^+$ dans [34]). La raison est à trouver dans les déformations Jahn-Teller du système. On peut alors introduire un modèle du << jellium >> déformé, à l'aide de paramètres d'ensemble correspondant aux plus bas moments multipolaires de la distribution de charge positive $\rho_{\rm jel} ({\bf r})$. Cette amélioration est, elle aussi, insipirée par le modèle effectif de Clemenger-Nilsson [1]. Les premiers auteurs à avoir introduit un << jellium >> déformé, dans ce cas à déformation sphéroïdale, sont Penzar et Ekardt [35]. Ainsi, nous avons choisi pour $\rho_{\rm jel} ({\bf r})$, l'adoucissement de la surface étant pris en compte par une forme de type Woods-Saxon :

$$\rho_{\rm jel} ({\bf r}) = \frac{3}{4\pi r_s^3} \left[1+\exp{\left(\frac{\big\vert{\bf r}\big\vert-R}{r_c\sqrt{3}}\right)}\right]^{-1}$$ (8)

avec $R$ qui tient compte de la déformation (ici pour simplifier à symétrie axiale, comme dans [36,37]) du << jellium >>

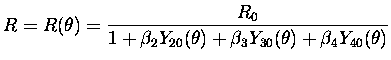$$R = R(\theta) = \frac{R_0}{1 + \beta_2 Y_{20}(\theta) + \beta_3 Y_{30}(\theta) + \beta_4 Y_{40}(\theta)}$$ (9)

la déformation étant insérée par les harmoniques sphériques $Y_{l0}$ et son amplitude par les coefficients sans dimension $\beta_l$. Le rayon $R_0$ est proche du rayon du << jellium >> abrupt $R_0 \simeq r_s N^{1/3}$ obtenu à partir du rayon de Wigner-Seitz $r_s$ ($R_0$ est légèrement réajusté pour avoir le bon nombre de particules $N$ ). Le paramètre de largeur de surface dans Eq.(I.8) est déterminé par le rayon de cur de $r_c=1.73{\rm a}_0$ d'un pseudopotentiel de Ashcroft ; les effets de compression des agrégats les plus petits sont négligés et nous prenons $r_s=4\,{\rm a}_0$, c'est à dire le rayon de Wigner-Seitz du solide de sodium infini.

L'introduction du << jellium >> déformé permet alors de rendre compte de la fragmentation d'origine géométrique observée dans les spectres de résonance électronique dans les agrégats non-magiques.

Le modèle du jellium donne ainsi, moyennant certains raffinements, des résultats acceptables pour le sodium, mais il reste entaché de déficiences irrémédiables. Le calcul de l'énergie de constitution de l'agrégat est très malaisé, or cette valeur est indispensable lorsqu'on cherche les structures d'équilibre. On peut introduire cette énergie grâce au SAJM (Structure Averaged Jellium Model, [38]), mais l'absence de prise en compte explicite de la structure ionique a des conséquences manifestes sur les spectres de photoabsorption à basse température, comme nous l'avons déjà souligné à propos de la figure I.1. Par ailleurs, le modèle du jellium ne convient vraiment bien qu'au cas du sodium, et il est manifestement très difficile de coupler la dynamique des ions à celle des électrons dans ce cadre. Nous avons donc introduit dans notre modèle des pseudopotentiels simples pour les atomes de sodium.