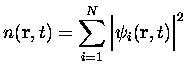 |
(5) |
Dans les paragraphes précédents, nous avons rappelé les principaux points de la théorie de la fonctionnelle de la densité, pour l'état fondamental d'un système d'électrons en interaction. Or, dans cette thèse, nous nous attachons à simuler en temps la réponse des électrons de valence d'agrégats à des perturbations extérieures. Il faut donc utiliser une extension de la théorie de la fonctionnelle de la densité aux phénomènes dépendant du temps. Cette extension a essentiellement été formalisée et mise au point dans les travaux de E.K.U. Gross et ses collaborateurs ; nous allons en reprendre la formulation qu'il donne dans [31]. Nous donnons plus de détails dans l'annexe B.
Pour un système de fermions en interaction évoluant à partir d'une certaine fonction d'onde initiale, on peut établir comme dans le cas statique des équations à un corps, et la densité du système peut être obtenue par
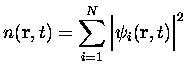 |
(5) |
avec
![]() le potentiel extérieur et
le potentiel extérieur et
![]() le potentiel coulombien classique.
le potentiel coulombien classique.
Cependant, comme dans le cas statique, le problème de
départ B.4 n'a été en quelque sorte que reformulé : il faut
trouver une approximation de
![]() .
.
L'approximation la plus simple, celle que nous allons employer dans la suite de ce travail, est celle de la << LDA adiabatique >> : elle consiste à employer la forme fonctionnelle de la LDA avec une densité dépendant du temps, c'est à dire une approximation locale en espace comme en temps.