Etude détaillée de Na$_9^+$

Dans les chapitres précédents, nous avons présenté les résultats obtenus avec différents fonds ioniques (<< jellium >> ou différents pseudopotentiels), à chaque fois sur l'exemple particulièrement simple de Na$_9^+$. Les calculs sont particulièrement facilités dans ce cas par le fait que, par son nombre << magique >> d'électrons de valence, cet agrégat présente une structure quasiment sphérique. On peut alors restreindre le nuage électronique à la symétrie axiale. De plus, comme il est positivement chargé, ses électrons de valence sont un peu plus liés que dans Na$_8$ ; l'étude dynamique est donc peu perturbée par les éventuelles fuites d'électrons par suite du dépôt d'une certaine énergie d'excitation dans le système.

Afin de pouvoir comparer les résultats obtenus avec restriction à la symétrie axiale et ceux obtenus en trois dimensions effectives, nous allons prendre comme fond ionique la structure 144 obtenue par la méthode CAPS [38], qui suppose une symétrie axiale du nuage électronique. Cette structure est représentée sur la figure III.1 : elle est très proche de celle obtenue grâce à la méthode de Car-Parinello par les auteurs de [61]. Les pseudopotentiels ont également la même force que dans [38], voir l'annexe E. Comme dans la plupart des autres calculs que nous avons réalisés sur cet agrégat, nous avons pris une grille de $48\!\times\!48\!\times\!48$ points espacés de $0.8\,{\rm a}_0$.

On peut noter que le nuage électronique de l'état fondamental tridimensionnel obtenu avec cette structure ionique adopte une forme très proche de la symétrie cylindrique, ce qui contribue a posteriori à prouver la validité des hypothèses du modèle CAPS. Nous donnons sur la figure II.1 page  des surfaces d'isodensité électronique de ce nuage, et une coupe transversale à travers le nuage qui confirment cette symétrie axiale.

Figure III.2: Spectres de puissance des moments dipolaires pour ${\rm Na}_9^+$ avec la configuration CAPS 144. Les graphes du bas ont été obtenus dans le régime linéaire, ceux du haut dans le régime non-linéaire. Les graphes de droite correspondent à une excitation suivant l'axe de symétrie $z$, et incluent les résultats d'une étude dynamique restreinte à la symétrie axiale. Ceux de gauche correspondent à une excitation suivant la direction $x$. Dans tous les cas les moments dipolaires ont subi un filtrage dans le domaine temporel.

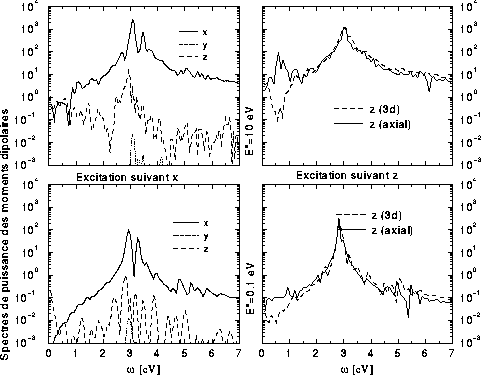
Les spectres de puissance obtenus après diverses excitations de ce nuage électronique sont présentés sur la figure III.2. Les deux graphes de droite y montrent les spectres du moment dipolaire suivant $z$ (l'axe de symétrie), obtenus après excitation par une translation instantanée du nuage électronique suivant ce même axe $z$. Les courbes en pointillé représentent le résultat obtenu par le calcul restreint à la symétrie axiale, celles en trait plein les spectres obtenus par la méthode tridimensionnelle.

Les graphes inférieurs représentent les cas des petites excitations, avec une énergie d'excitation de $E^*\!=\!1\,{\rm eV}$. Les deux spectres de puissance coïncident correctement en ce qui concerne la position et la largeur du pic plasmon.

Le graphe supérieur représente le cas d'une excitation plus violente où l'énergie d'excitation atteint $E^*\!=\!10\,{\rm eV}$, correspondant à trois fois l'énergie du plasmon. On peut voir là aussi que les résultats des deux méthodes sont en très bon accord. Les degrés de liberté ouverts en trois dimensions ne changent donc pas la structure de la résonance. En particulier, ils n'ajoutent pas de dissipation supplémentaire, et les conclusions de nos travaux [21,22] restreints à la symétrie axiale restent valide, à savoir que la résonance plasmon est un mode extrêmement harmonique, qui présente peu d'effets non-linéaires tels que la génération d'harmoniques doubles ou une transition vers le chaos. Les deux graphes de droite de la figure III.2 confirment donc a posteriori la validité des études restreintes à la symétrie axiale, en ce qui concerne le mode suivant $z$.

Les graphes de gauche de la figure III.2 montrent les spectres de puissance pour une excitation orthogonale à l'axe de symétrie, ici dans la direction $x$. Les moments dipolaires dans les trois directions cartésiennes ont été représentés pour étudier le couplage entre les modes. Dans le régime linéaire (en bas) il est clair que l'excitation suivant $x$ produit de façon prédominante un mode suivant $x$. Par rapport à la même excitation suivant $z$ (à droite), on peut voir des différences dans le détail des spectres ; la résonance se manifeste par un seul mode clair suivant $z$ alors qu'elle est fragmentée suivant $x$. Ces différences seraient absentes si on avait pris un fond de << jellium >> sphérique. La fragmentation du mode suivant $x$, due à l'interférence avec une monoexcitation électronique d'énergie proche de la résonance plasmon, est donc un effet de la structure ionique (nous parlions de cet effet, discuté dans [19], page ).

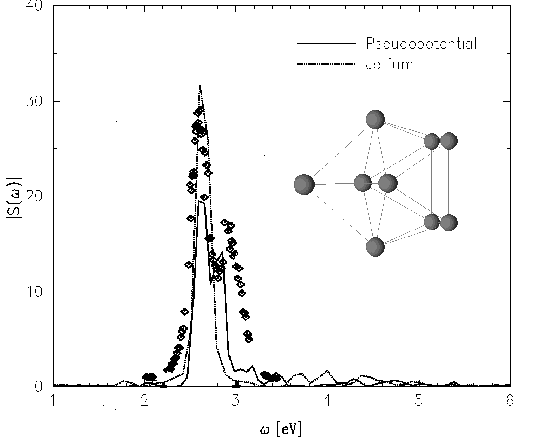
La structure ionique génère en effet une distribution de monoexcitations électroniques RPA plus dense au voisinage de l'énergie du plasmon que celle obtenue avec un << jellium >>, où la valeur propre RPA la plus proche de l'énergie du plasmon a une énergie de 4 eV, même lorsqu'on introduit un moment octupolaire équivalent à celui de la distribution 144. Un calcul tridimensionnel avec structure ionique détaillée est donc indispensable pour reproduire la fragmentation des spectres observée dans les expériences fines à basse température, comme celles dont nous représentons les résultats sur la figure III.3.

Figure: Partie imaginaire de la transformée de Fourier du moment dipolaire d'un agrégat Na$_9^+$ obtenue avec un fond ionique explicite, des pseudopotentiels locaux ayant une force de 49,97 (voir annexe E), excitation dans le régime linéaire, calcul dans le domaine temporel de 10000 itérations de 0.1 unités Hartree (48 fs), filtrage de la transformée. La configuration ionique utilisée, calculée par optimisation tridimensionnelle, est présentée en haut à droite. Les détails de la procédure d'excitation sont présentés page 

Pour une excitation dans le régime nonlinéaire suivant $x$,(en haut à gauche sur la figure III.2) on voit que le découplage des modes entre $y$ et $z$ est essentiellement maintenu. L'harmonicité du mode plasmon dans ce modèle est donc confirmée. Nous donnons sur la figure III.3 le spectre ${\cal S}(\omega)=\Re\left\{\tilde{D}(\omega)\right\}$. Ces spectres représentent la somme avec des poids identiques des moments dipolaires suivant les axes $x$, $y$, et $z$ obtenus après excitation du nuage électronique suivant la diagonale $(1,1,1)$. En effet, dans un montage expérimental, il n'est pas possible de contrôler l'orientation des agrégats soumis à une impulsion laser femtoseconde par exemple. Comme nous avons montré dans l'étude détaillée de Na$_9^+$ que les trois modes de base étaient essentiellement indépendants, en particulier dans le régime linéaire, nous pouvons simuler la superposition incohérente de ces modes dans un seul calcul TDLDA par cette excitation suivant la diagonale. C'est ce qui a été fait dans les calculs dont les résultats sont présentés sur la figure III.3, l'excitation déposant moins de 0.5 eV dans le système, qui demeure donc dans le régime linéaire.

Sur cette figure III.3, nous comparons le spectre obtenu dans le régime linéaire à des résultats expérimentaux pour la section efficace de photoabsorption obtenus avec des sources lumineuses de puissance relativement faible, ce qui correspond dans nos calculs au régime linéaire. Le spectre du moment dipolaire obtenu par ce processus d'excitation, moyennant un facteur d'échelle caractérisant l'amplitude de l'excitation [23], peut alors se comparer directement à l'expérience. On voit que les deux pics qui apparaissent dans le spectre expérimental sont reproduits correctement ; de tels résultats ont également été obtenus par les calculs ab initio dont les résultats sont donnés dans [3], ou par la méthode de << perturbation par pseudopotentiel >> de [62]. Le modèle du << jellium >> dont les résultats sont donnés sur la figure III.3, est incapable de rendre compte de cette fragmentation du pic, comme nous l'avons discuté plus haut.